
Summary from the Computational Thinking for Problem Solving course from Penn Engineering.
This are the 4 pillars to approach problems more systematically, developing more efficient solutions, and understanding how computers can be used in the problem solving process.
Computational thinking involves using concepts from computer science to develop solutions to problems. But it also involves expressing those solutions in such a way that they can carried out by a computer.
Decomposition
Decomposition is the process of taking a complex problem and breaking it into more manageable sub-problems. You can also consider a sub-problem as another complex problem and further decompose.
Pattern Recognition
When we decompose the problem, we frequently find patterns among the sub-problems, i.e., similarities or shared characteristics. Discovering these patterns make the complex problem easier to solve since we can use the same solution for each occurrence of the pattern. We use pattern recognition in solving everyday problems such as repetitive drawing tasks or mulching a garden.
Data representation and abstraction
Data representation and abstraction involves determining what characteristics of the problem are important and filtering out those that are not. From this, we can create a representation of what we're trying to solve. Information is important may vary depending on the task objective.
Algorithms
An algorithm is a set of step-by-step instructions of how to solve a problem. It identifies what is to be done (the instructions), and the order in which they should be done.
YOu can use the help of a flowchart to describe the algorithm in a high level.
Algorithms complexity
-
When we analyze algorithms, we consider the number of steps or operations that need to be performed as a function of the input size.
-
A linear algorithm is one in which the number of operations increases linearly with the increase in input size.
-
We consider complexity in the worst case so we can see the change in operations when the input size changes.
Common algorithms
Linear search
A linear search is when we look at all the values once. We have to do this because the list is not ordered.
Binary search
The list needs to be ordered.
We can also describe the algorithm binary search using a flowchart. We start by taking its input, the list and the target element. If the list is empty, then we can stop and output false. The element is not in the list. Otherwise, we look at the middle item in the list and compare it against the target. If it is the target, then we can stop and output true, we have found the element. Otherwise, if mid is less than the target,then we eliminate mid and the first half of the list. If mid is greater than the target, then we eliminate mid and the second half of the list. We repeat this process until the list is empty.
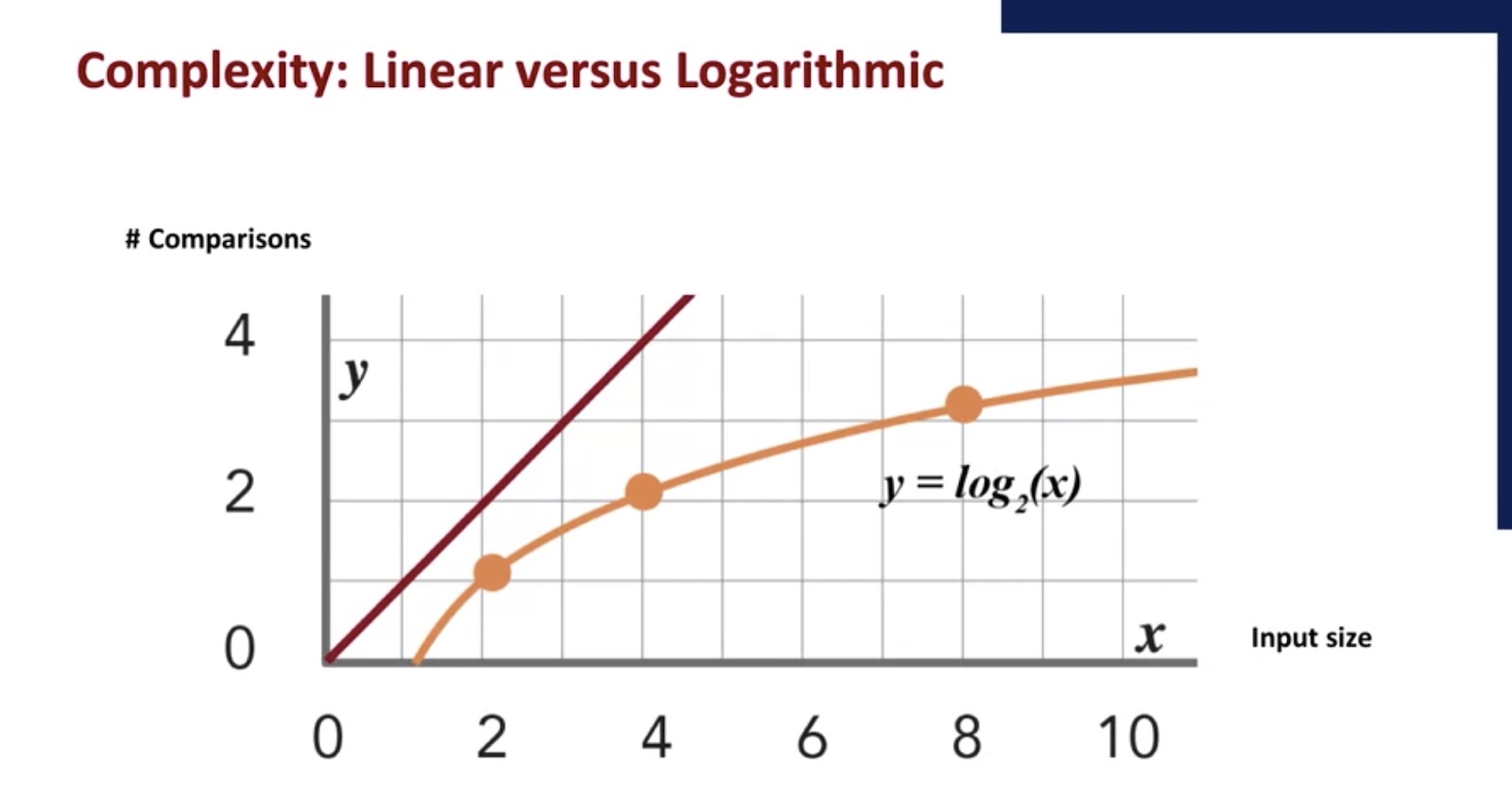
In this graph, we show the difference in behavior between linear search shown here in red, versus binary search, shown here in orange. Here, the x-axis is the input size. And the y-axis is the number of comparisons.
In linear search, if you double the size of the input, say from 2 to 4, the number of comparisons doubles. But with binary search, after each comparison, you eliminate half the list. So if you double the size of the input, say from 2 to 4, the number of comparisons only grows by 1.
Algoritms general approaches
Brute Force algorithms
Many problems that we encounter in computational thinking involve taking a list or a collection of things and organizing them in some optimal way or finding some optimal subset of things from the list. When it comes to these sorts of optimization problems, finding not just a valid solution but the best solution, one approach that will always work is to try all possible solutions and choose the one that's best. After all, if you consider all the possible solutions, then you know for certain that at least one of them will be the one you're looking for. This is known as a brute force approach.
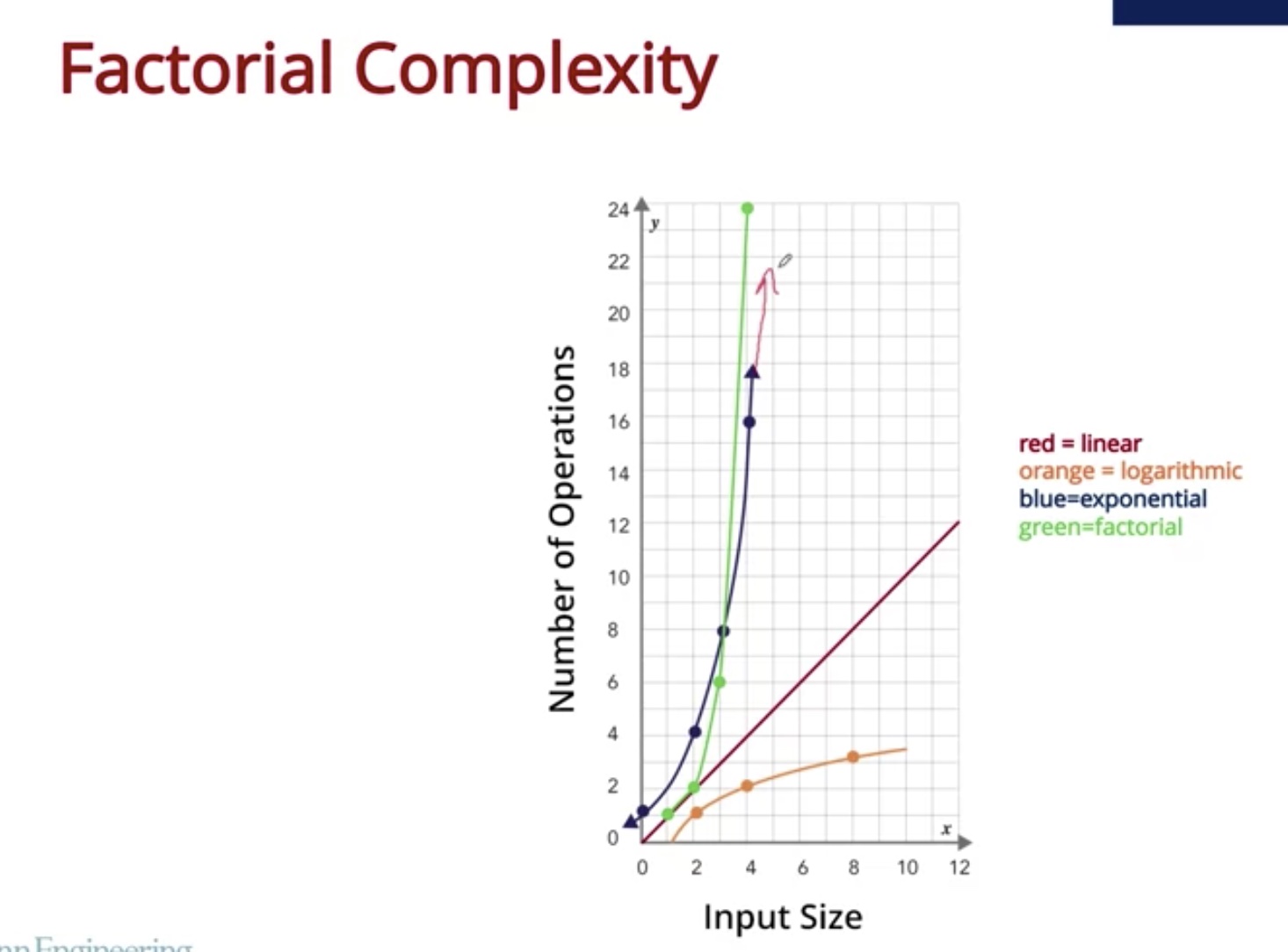
But in many cases, this can result in a huge number of possible solutions, which may be exponential or factorial with respect to the number of options.
Greedy algorithms
In a greedy algorithm you do the thing that seems best at the time or locally optimal as we say and it's going to get you closest to solving the problem even if it's not actually part of the best solution.
It's kind of the opposite of brute force. With brute force, you look at all the possibilities and then choose the one that's best. In a greedy algorithm, you just say, I'll do whatever seems best right now, repeat, and hope it all works out later. Greedy algorithms are not guaranteed to give you the optimal solution, but in many cases can quickly give one that may be good enough.
It may not always give the best solution but at least it's quick and may give us something that's close to optimal in much less time.